Seeing triangles in dots

Figure 1

In developing their theory of Boolean maps at reference 1, Huang and Pashler talk of what happens when we are asked to focus on the white, red and yellow spots in Figure 1 (part of their Figure 5), with the proposition being that when we focus on the three spots concerned, we will probably be aware of their making a triangle and will probably be aware of little else, at least so long as our attention is indeed on those three spots collectively. Another part of the proposition is that the three spots collectively do have position but do not have colour, although had they all been the same colour, they would have had.

We consider here what might happen here in the world of LWS-N, most recently figuring at reference 2. With our concern not being whether the Huang and Pashler proposition is true or not – with its success with us seeming to depend on the size of the picture and with the occasion – but rather with what LWS-N would do with such a triangle in the event that it was. Or to be more accurate, what the LWS-N compiler would do with it. We think that the answer is in three layers, as follows.

Figure 2

Figure 2 is the triangle part of the content of consciousness, in its own layer. A four part layer object (in blue), with the interior of the triangle not having a texture net (in green) and so not being activated, while the vertices with their interiors and the perimeter of the triangle are.

Figure 3

A slightly different way of doing the triangle is shown in Figure 3 above, a seven part layer object. Here, the sides of the triangle have been promoted to parts of the layer object in their own right, with their own texture nets, just one of which has been sketched in. Not much idea yet as to how one might choose between Figure 2 and Figure 3. Perhaps just two different ways of experiencing the triangle, with the compiler going for one or the other according to circumstances.

Note that in neither Figure 2 nor Figure 3 is there any colour. There are texture nets to give substance and activation, but substance without colour. Perhaps texture nets without any regularities, so activation without anything more, without any internal structure.

Figure 4

While Figure 4 is a simplified version of the original coloured spots, with the spots of interest duplicated and marked with a red node, a colour which would not be expressed on the ground, in LWS-N, and is just used here as a prop. One might add a further texture net to colour in the background.

We have not troubled to vary the texture nets (in green) that we do have to express the colours of the various spots, but that is how it would be done. Something regular and uniform, perhaps some kind of repetitive tiling, something different for each colour.

All these spots being on their own layer, simplifies – perhaps eliminates – unhelpful interaction between the triangle and the spots not on the triangle.

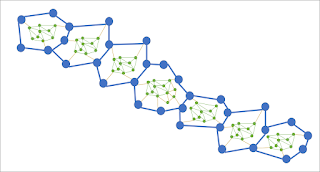Figure 5

 There might be a third layer to carry the information that the figure 2 is a triangle, linked by a column object to that triangle to ensure concurrent activation. Perhaps Figure 5, a six part layer object, expresses a six letter word meaning triangle. The jury still being out on exactly how this is going to be done. Maybe this layer object would express the sound of the word in question rather than its written form. Maybe the code for motor actions needed to sound the word, silently or otherwise.

The compiler could adjust the relative level of activation of these three layers according to person and circumstance.

Some preliminary thoughts about texture nets

We have already suggested that a random texture net, without any significant regularity or repetition might be used to signify presence and position without anything else.

Even a net which is random in detail can vary in space, both as regards density of nodes and activation. Such nets might well code for something.

Otherwise, the first idea is that regularity and repetition are used to signify things like colour, tone (in music), smell and so on.

Figure 6

Maybe the sort of thing we have in Figure 6 would do for colour – bearing in mind that this picture of repetitive tilings was thrown up by Bing and the colours therein have nothing to do with our texture nets – nor do colours have any place in a texture net, where there are no colours in the ordinary sense of the word. But we do have fourteen distinct tilings, which serve to show off some of the things that can be done. The idea being that activation of the fourteen corresponding texture nets would yield fourteen distinct subjective experiences.

A caveat being the fact that in Figure 6 we have some improper vertices, that is to say one line meeting another line somewhere other than at a corner. So all four tilings on the bottom row do this. A wrinkle that needs to be ironed out.

The idea also being that the right sort of texture net, through its activation (which has been put together by the compiler) is colour. It is not a label saying ‘colour’, it is not a pointer to such a label, it expresses colour, it represents colour in itself.

However, we suspect that colour will be actually be expressed by very simple texture nets, rather simpler than those of Figure 6, because colour can vary a great deal in space and we need to be able to give colour to quite small patches of space. This is less true of music and even less true of smells. So if we close our eyes, a smell might be allowed to occupy quite a large proportion of the space available in LWS-N.

Figure 7

Figure 7 shows a simple triangular net, spanning the space it occupies in a regular way. In this case, equilateral triangles, all of the same size and with just two orientations, up or down.

Figure 8

Here we have sketched a mixture of squares and right triangles, each triangle being a quarter of a square. Four orientations for triangles, just the one orientation for squares. We do not require the squares and triangles to be exact and we suppose that an approximation in space will suffice, with the subjective experience degrading with the approximation.

There are all kinds of other possibilities here, with the number of possibilities rapidly increasing as we allow more complicated mixtures.

A worry here is that while this geometry is expressive, is plausible as a vehicle for the subjective experience, it is not very neural. Neurons might have positions on our bit of cortical sheet, but is it plausible that their synaptic connections will aggregate up in this nice neat way into triangles and squares? Even if we pay more attention to the graph than to the position of the nodes in space?

So the second idea is that rather than using geometry, as in the foregoing, we use statistics. So we might, for example, regard the density of nodes as a key variable. Or the average number of links per node. Or the average length of links. These all being variables which do not depend on the net being planar and which might vary in a modest way across the extent of a texture net. And with a bit of imagination one can come up with lots of such variables, some more plausible than others.

The third idea is that rather than just having one sort of node and one sort of link, we allow a small number of each, perhaps three sorts of node and three sorts of link; a sort of alphabet. Combinations then give us lots of possibilities.

The fourth, and so far last, idea is topology. So far we have a planar texture net suspended in a part, in a hole in a planar shape net. We might go further and allow texture nets to have more complicated shapes, but restricting them to the representation of smoothly curving two dimensional sheets in three dimensional space. All the nodes would be in the plane of our bit of cortical sheet, but the graph would suggest three dimensions, would embed nicely into three dimensions. We do not pursue these possibilities here.

So geometry, statistics, alphabet and topology – so far. Four ways of jointly exploiting the position (geometry) and connections (graph) of our neurons to give some body, some life to our shape nets. Some of which is not that different from the soft centred patterns of the now obsolete LWS-W; not surprising as we address the same problem of how to inject some content and meaning into fairly simple data structure. See references 5 and 6.

Modality

We see texture nets as a general purpose device for the expression of all the senses, all the stimuli coming into the brain – noting that reference 4 argues that that is all there is. Anything which gets coded up in the brain takes the form of stuff coming in from one or other of the senses.

So we need to sort out how we are to distinguish the various modalities, what it is that distinguishes the various modalities – sight, sound and so on – bearing in mind that there are some people – synaesthetics - who get fairly muddled up in this department. The distinguishing features, whatever they might be, need to be able to break down.

A first step might to be to identify some candidates for such distinguishing.

Conclusions

We have offered some suggestions as to how LWS-N might code up Huang and Pashler’s triangle and digressed onto the business of texture nets more generally, albeit in a very preliminary way.

We will be talking more about texture nets in due course.

References

Reference 1: A Boolean map theory of visual attention - Huang, L., & Pashler, H. – 2007. Abstract: a theory is presented that attempts to answer two questions. What visual contents can an observer consciously access at one moment? Answer: only one feature value (e.g., green) per dimension, but those feature values can be associated (as a group) with multiple spatially precise locations (comprising a single labelled Boolean map). How can an observer voluntarily select what to access? Answer: in one of two ways: (a) by selecting one feature value in one dimension (e.g., selecting the colour red) or (b) by iteratively combining the output of (a) with a pre-existing Boolean map via the Boolean operations of intersection and union. Boolean map theory offers a unified interpretation of a wide variety of visual attention phenomena usually treated in separate literatures. In so doing, it also illuminates the neglected phenomena of attention to structure.

Reference 2: https://psmv3.blogspot.com/2018/05/a-modest-change-to-layer-objects-of-lws.html.

Reference 3: http://psmv3.blogspot.com/2017/07/binding.html. Includes some discussion of column objects, albeit in the context of LWS-W rather than LWS-N.

Reference 4: The Mind Is Flat: The Illusion of Mental Depth and the Improvised Mind - Nick Chater – 2018. To which I owe reference 1 and the whole triangle story.

Reference 5: https://psmv3.blogspot.com/2017/03/soft-centred-patterns.html.

Reference 6: https://psmv3.blogspot.com/2017/04/shapes-not-numbers.html.

Group search key: srd.