This post is the first of what is intended to be a short series, with this one being preparatory in nature. The end-game is a conscious homunculus – for background on which see reference 1.
Suppose we have a grid, a square array of integer values, a large array containing millions of points, thought of as being defined over some small patch of the cortical sheet of a higher animal, probably a human, with those integer values being in the range [0..N] where N is some not very large number, probably less than 20, the number of bands of power of brain waves, at the frequency that we are looking at, that we can reasonably work with in the particular bit of brain that we are looking at.
We are looking for some way of defining objects on our square array, objects which have shape: that is to say they are relatively simple, often convex, always connected regions of the grid. Regions with a boundary and an interior – including here long thin regions which might be considered as lines, or at least linear.
But we do not have the paraphernalia of geometry or of drawing packages, let alone a pencil and paper: all we have to go on is our square array of values, on which we propose to use patterns to define objects, objects which are something like the shapes one can create with Powerpoint. Objects which might well take recognisable shapes: lines, circles, houses and animals.
We suppose that repetition of some sort is the key, partly because we believe neuronal processing to be good at spotting repetition.
In what follows we look at how we might come up with a regime in which such objects might be defined, might be exhibited in some particular state of our grid.
A taster
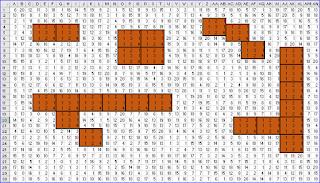
In the snap (taken from Excel) above, we have used a pattern defined on a three by three square of values and we looked around the grid for repeating patterns in order to build those repeats up into objects, with the idea being that we keep adding squares with the pattern, which conform to the pattern and which touch a square that we have already, until there are no more, until we can go no further. With the proviso that there must be at least two squares to count as an object, for us to be sufficiently confident that we are not just looking at noise. In the snap, we have five objects defined on the one pattern.
Variations might be to allow patterns to be defined on rectangles. To restrict the concept of touching, perhaps to sharing a whole side. To have rules about the size of rectangles, perhaps to exclude the degenerate case of the single point. Or we might loosen things up and allow patterns which nearly repeat, rather than just those which exactly repeat.
Finding the bits of pattern in this snap which do not amount to objects is left as an exercise for the reader.
Some rules
As we suggest above, there are lots of ways of doing this sort of thing, but we want, we need to narrow things down a bit and to pick one. To define the regime that we are going to work with.
We define patterns of points on our grid and we then define a simple process for generating objects from those patterns.
We will base our patterns on small rectangles, probably containing 25 points or less. We imagine that there could be hundreds of patterns of this sort, a lot more than one is likely to want on just one grid. But we will have lots of grids and patterns are to be global.
If we place our pattern on the grid, rather as one might place a window on a waveform, we can say whether or not that patch of grid conforms to the pattern. We will have some more rules about conforming.
We link conforming patches which touch into objects. We will have some more rules about touching.
For any one pattern, we can then partition our grid into zero, one or more disjoint objects taking that pattern, plus a remainder, a background.
If we allow a number of patterns, and we have a rule or a result which says that a point on the grid can only participate in at most one pattern, we can still partition our grid into zero, one or more disjoint objects, with each one taking one of those patterns, plus a remainder, a background.
Sometimes the objects will cover the grid and there will be no background left; or at least the background will have been patterned over – perhaps giving it a texture or a colour. Plus, our objects are labelled by the pattern on which they are built. We call objects built on the same pattern, peer objects.
What rectangles?
In the example above, our rectangle has been a three by three square, giving us 9 points. Other things being equal, the bigger the rectangle the less likely it is that any repetition of our pattern is down to chance. Repetition will nearly always be significant.
On the other hand, it would make things very simple to go down to a single point, a one by one square. This maximises the resolution of our shapes, our objects, but minimises our ability to label them. And maximises the possibility of disturbance, of the creation of false structure, by noise.
We propose allowing rectangles of any shape or size, with the only proviso, as noted above, that they are usually less than around 25 points in all.
In any one pattern, the rectangle, of whatever shape it may be, will always be orientated the same way. In the case of a square, for example, we do not allow rotation of our pattern of values.
We might insist that our rectangles tile the grid in a nice simple way, that we divide the grid into rows and columns which yield cells of the required size. Which might turn out to be a simplification which does not cause too much pain elsewhere – but we have not so insisted in the example illustrated above.
Defining patterns on rectangles
In the example illustrated above, our pattern has been defined by exact match by position. Each point on the square on the grid has to have the right value. This has the virtue of simplicity and it may well be that it is as easy for neurons to pick out such patterns as it is for the eye.
But there might also be merit in loosening things up a bit.
We might allow wild cards. We might say that positions where the pattern has a zero can take any value.
We might say that we just have a list of values and the points in a conforming rectangle must take all of those values, but without caring about position of those values within the rectangle. Such a list might be of the form {2,5,6}, with distinct values, or it might be of the form {3*2,5,3*6}. Here we are saying that our rectangle must contain 3 two’s, 1 five and 3 six’s.
We might allow ranges rather than matches. For example, the point at this position must have a value which is greater than 2 and less than 8.
We might allow a proportion of misses. The patch conforms provided it matches in at least so many of its positions.
Rules about touching
We start with a seed for our object, a rectangle at which we have a conforming pattern. We then grow that seed by adding conforming rectangles which touch one or more of those that we already have. We carry on adding until there are no more to be added. An object is maximal in that sense.
The most strict rule would be to say that two rectangles touch if they share an entire side.
We might weaken that to say that two rectangles touch if they share a good part of a side.
We might weaken that so far as to say it suffices if our two rectangles share a point – thus allowing the diagonal connection at the bottom of the bottom left example above.
It is possible that one could do something with rectangles which overlapped, with one partially overlapping the other. This option is not pursued here.
We believe that rules of this sort will generate well defined objects. That one will, for example, get the same object regardless of the seed chosen to generate it. That one will get the same object regardless of the order in which one adds touching rectangles. We suppose that one could devise candidate regimes for which this was not true.
There would be merit from a touching point of view in using regular hexagons rather than rectangles, but that would complicate things from other points of view and this option is not pursued here.
Our objects have to be connected by touch. But we note the case of a real world object whose mapping onto some two-dimensional bit of space has become disconnected, perhaps a bicycle which happens to have been cut in half by a lamp post in front of it. We will suggest a way to deal with this in one of the posts which follows.
Specifying a pattern
Whatever rules along these lines we come up with for patterns, given those rules, given that regime, it will be possible to specify any pattern by a string of integers, a string of fixed length and format, probably less than 50 integers or so long.
We do not require that all such strings code for valid patterns, but we do require that we can tell which ones do and which ones do not.
These strings will, in some sense, label the objects which are defined on the pattern in question. We might call them the key to the pattern.
Given a grid of values and a regime, we suppose that it would be straightforward to devise an algorithm, to devise code which would search that grid for patterns and objects. It might take a while to run in Visual Basic on a laptop, but it would run. And it could, in principle, run a good deal faster in a brain.
It is possible that we will want to define simple relations between such strings, perhaps to define hierarchies and networks, but we do not pursue that possibility here.
By way of example, suppose our regime consists only of three by three squares with exact match. Then a specification of any pattern conforming to that regime could be specified in a string of nine integers, with each integer specifying the number the pattern took for one of the positions of our square. But remember that this specification of a pattern is regime dependant; you cannot mix or compare patterns from different regimes.
Odds and ends
A pattern might include saying how many repeats one has to have to qualify. So far we have said any repetition is good enough, but we might want to require more in the case of a small pattern, the sort of small pattern which might turn up by chance it what is otherwise noise.
What with one thing and another, we have to allow, at some point, for the possibility of false positives, of repeats in the data which do not carry any meaning, which are not supposed to be there. Which are just noise.
We might find significance in a value, in a power, being big rather than small. While the bins into which power is classified have in the foregoing mostly just been used as labels, much in the way that written labels might be, these bins are also ordered in an obvious way, with this numeric order being something stronger, less conventional than alphabetic ordering: the bins are not just sat around a table, not even a round table. Big bins reflect high arousal and attract attention – but more of this in the posts to come.
There might be a natural partial order on patterns. Such a partial order might map onto sequences such as Judy’s pet rabbit, rabbits in general, furry animals and quadrupeds.
There might be a metric on patterns. This pattern is so far from that pattern. Such a metric might be useful in the case that we did not insist on exact replication. Or in that when we have noise in our data array.
Conclusion
It is possible to come up with a regime which defines a class of patterns and which enables us to build well defined objects on our grid from those patterns which meet our requirements, with, for example, distinct objects being disjoint. It may not be necessary, at least in these early stages, to be much more specific.
Reference 1: https://en.wikipedia.org/wiki/Homunculus_argument.
Group search key: sra.
No comments:
Post a Comment