From neurons to layer objects

We have a patch of cortical sheet which we hypothesise to contain the entire content of consciousness and activation of which is further hypothesised to generate the subjective experience of consciousness.

One aspect of this is that the patch has to be entirely self-contained. It cannot draw its meaning and significance from somewhere else, it all has to be there, of itself. The first stab at this, dubbed LWS-W, was conceived as layers of worksheet, rather as if the various worksheets of an Excel workbook had been piled, one of top of another. The second stab at this, dubbed LWS-N, was conceived along more obviously neural lines, with the core structuring device being the graph rather than the array. Nevertheless, the concepts of layer, layer objects and their parts were retained.

Here, we pull together the introductory material at references 1 and 2, as updated by reference 6, to more fully define layer objects and related concepts in our world of LWS-N, our local (or layered) workspace. In this, we use adapted versions of some of the figures in reference 2. A fuller description of all these various posts, as at the end of May, is given at reference 7.

We do not expound on the work to which these concepts will be put. That will follow in posts to come. Nor do we expound on how the successive frames of LWS-N are put together, are compiled. Our present interest is the specification of the container, not in the contents or how they get there.

Figure 1 below is a simple version of the model which we will develop in what follows.

Figure 1

Layers are made of layer objects, defined in large part by shape nets. Shape nets, as their name suggests, define the shape, in the ordinary sense of the word, of layer objects arising from vision. They also, in large part, define the breakdown of layer objects into their parts. Parts which will often contain texture nets, nets which, in the case of vision, serve to give our objects colour and texture.

This despite the belief of most neurologists that the topical organisation of vision breaks down fairly early on in the visual processing chain (with the eye here counting as upstream and consciousness as downstream), not least because of the great divide into dorsal and ventral steams. See, for example, the introduction to reference 9. The contention here that it is all pulled back together into a topical organisation for the purposes of, or at the very least, at the time of, projection into consciousness.

Neurons

We start with neurons and synapses, with a few million neurons and rather more synapses embedded in our two dimensional, unit square of cortical sheet.

We aggregate these neurons and synapses into a rather smaller number of nodes and links; nodes and links which make up the graphs of the world of LWS-N. We show two nodes and one link in the top part of the figure below.

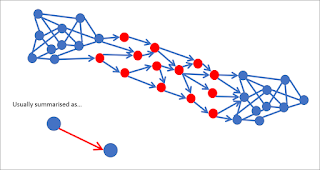Figure 2

Nodes

A node is a strongly connected set of neurons. Every node has a small, circular neighbourhood, containing all its constituent neurons, with the centre of that circle being regarded as the position of the node. It might be appropriate to think of these neurons as having short axons, only needing to span their host neighbourhood.

Nodes come in two flavours: shape nodes and texture nodes. Roughly speaking, shape nodes are bigger and stronger than texture nodes.

Nodes have weights, perhaps nothing more complicated than the number of constituent neurons.

At any point in time, a node may be active, by which we mean that the number of firings in some small neighbourhood of that time is significantly higher than the baseline rate of firing.

Now we have hypothesised that consciousness arises from the electrical activity of the constituent neurons of our bit of cortical sheet, which we take to mean the action potentials generated by those neurons rather than anything else more tricky. But we also suppose that the conscious experience is the result of some kind of integration, some kind of smoothing, and perhaps not dependent on the detailed timings of those action potentials or the phases of the imputed sinusoidals. This might mean, for example, that what counts is the frequency distribution of the firing over our bit of cortical sheet.

Figure 3, ex Sourceforge/LTFAT

So, at each position on our square of cortical sheet we might look to things like the figure above, the sort of analysis often done of audio signals, with frequency up the page, time across the page and with the strength of the corresponding part of the signal coded by colour. Remembering here that firing frequencies of neurons are rarely sustained at more than a few hundred Hertz, never mind a few thousand.

Links

A link is rather different. It is a set of neurons which are connected in a linear and directed way, carrying activation from one node to another. It might be appropriate to think of these neurons as having long axons, needing to span longer distances than those between the neurons of a single node.

Links may be unidirectional (aka directed) or bidirectional. In this latter case nodes are organised in such a way that if activation arrives on one link, it is passed on through the other links available, not back down the link on which it arrived.

Apart from direction, links come in three flavours: links which link the various elements of layer objects (O-links), links which link the various layer objects of a layer (L-links) and links between layer objects on different layers (C-links). With the layer objects on different layers being linked in this way being called composite objects and being discussed below.

The O-links also come in three flavours according to the use to which they are put: shape node to shape node (aka shape links), texture node to texture node (aka texture links) and shape node to texture node (aka mixed links), not distinguishing direction in this third flavour.

Generally speaking, the length of O-links, the distance between distinct nodes, is large relative to the diameters of either of the neighbourhoods involved, while C-links are short and L-links are somewhere in between.

Links have weights, again perhaps nothing more complicated than the number of constituent neurons.

Links may be active, perhaps taking the form of waves of activation travelling along the link, from source to target node.

Activation

We suppose that it is easy to trigger activation of nodes. Just poking a few of the neurons of a node will rapidly result in activation spreading through the node.

At a higher level we will talk of the focus of attention, the unit of activation, which may be a layer object, something larger (a composite object) or something smaller (a part).

And we similarly suppose that it is easy to trigger the activation of the focus of attention, with activation moving along the links from node to node. The wave of activation hits the node, pauses there for a bit, then moves into the link, then arrives at the next node. At the same time, another wave of activation goes across any corresponding texture net. With the directionality of the links involved being so arranged that poking a source node for the focus of attention, and there may be more than one of these, results in the activation of the whole. Notions which I think have something in common with the Boolean maps of reference 8, with one of the points of these last being that not all that much is active at any one time.

It may be helpful to talk about sinks and sources of activation.

We suppose that such activation, certainly within a layer, has a characteristic frequency. Maybe different layers are distinguished by being the harmonics of some base frequency, with the number of layers limited by the number of harmonics that we can experience.

Layers

We analyse the nodes into a number of disjoint layers, by some mechanism or device which we have yet to settle on. It may be enough to say that a layer is connected, in the sense that it is possible to get from any one node to any other, in one direction or the other, with L-links providing the links between the layer objects of a layer. While in the past, we had thought to define layers by the frequency of oscillation of their neurons when active, with frequencies being binned or banded into maybe ten bins or bands.

The C-links between layers are sparse. It is quite possible that any particular pair of layers, say A and B, are not linked at all. With the result that the links between layers are weaker than the links between the layer objects on a layer.

Such links as there are between layers are going to be vertical, in that the two nodes concerned will be in very nearly the same position. They will be short and will not have much visual impact on the layer networks. For the moment, any one node can participate in at most one inter-layer link. In this, we hark here back to the column objects of reference 3.

The graph expressed by the nodes and links in a layer will be more or less planar, which is to say that they can be embedded in a plane in such a way that there will be few links which cross each other. But see below for more on this point.

Maybe we will add a coefficient of connection for a collection of neurons, in this case a layer, which has to be more than some certain amount for the layer to be viable.

Layer objects

A layer object is a maximal set of nodes connected by O-links. As its name suggests, a layer object is contained within a single layer.

Roughly speaking, a shape net is a maximal set of linked shape nodes, all contained within the same layer, all linked by shape links. Shape nets are rather like the line drawings we make of the objects that we see, the objects that we build with the edges detected by the retina, but we also suppose their use to be generalised to other modalities.

In the simple case, a layer object is defined by its shape net, but there are more complex layer objects which include more than one shape net.

The shape nets of a layer are exclusive. The layer objects of a layer are also exclusive. They share neither nodes, links nor space. From which it follows that a layer is partitioned by its layer objects, possibly with a residual of texture nets which we call the background, the possibly large chunk of our cortical sheet not occupied by any shape net. And where there is no residual there is no experience of background; there is just nothing there.

We start with planar shape nets, but we may generalise that to nets which can be mapped onto the surface of a sphere, expressing three dimensional, but still relatively simple objects.
In the simple case, the parts of the shape net are its minimal loops. So in the figure below we have nine minimal loops defining nine parts, with no stray, superfluous bits of shape net.

Figure 4

While in the next figure we add some superfluous bits of net, superfluous in the sense that they do not usually perturb the division of the net into parts, but meaningful in the sense that they do change the pattern of activation, the subjective experience.

Figure 5

But there will be times when, for example, the spike bottom left will define further parts. Minimal loops will always define parts, but not always all the parts.

Shape nets go a long way to define layer objects and their parts – but we need to add texture nets to complete the story.

A texture net is a maximal connected set of texture nodes. The graph so defined is planar, with any texture net and any part of any layer object being topologically equivalent to a disc or a square. Any more complicated topology is expressed by the shape net. Texture nets are fine relative to the coarse shape nets, with a lot more nodes to the inch, as it were. Texture nets are exclusive. On any one layer, there can be at most one texture net in any one place.

A part of a shape net may contain nothing, another shape net or a texture net. That is to say, a texture net will usually be contained within a part of a shape net defined by a minimal closed loop, in which case it will be anchored to one of more of the relevant shape nodes. Texture nets will usually have lots of texture nodes, which we have not attempted in the examples which follow.

Figure 6

A simple layer object with two parts, each with a texture net, is illustrated above. The links, which are all O-links have been colour coded for legibility. They are also distinguished by the combination of nodes they link, with there being three combinations: shape node to shape node; texture node to texture node; and, shape node to texture node.

We expect, in the case of something which is seen, that the texture net will express the colour and texture of its part. And while we expect texture nets to be smooth and even in the way shown, we also envisage allowing them to vary across a part. Some texture nets will be made up exclusively of triangles. Some texture nets will be or will approximate to tilings, made up of regular triangles (that is to say equilateral triangles), regular quadrilaterals (that is to say squares) or regular hexagons.

Texture nets will also have sources and sinks. We will require at least one of the inbound links from the containing shape net to terminate in a source.

Figure 7

Figure 7 show a rather perverse two part layer object (A), with the left hand part containing a texture net and the right hand part, which does not have a texture net, containing a second two part layer object (B), in some sense or other. B is an object in its own right because there is no O-link connecting it to object A.

As it stands, Figure 7 is ambiguous: while the right hand part of object A frames object B, we are not told a great deal about the size or position of object B with respect to object A. An ambiguity which is a regular part of our visual world.

Figure 8, slightly adapted from Figure 7 of reference 6

Here, all the elements are connected by O-links and the layer object so defined is deemed to have two parts as there are two texture nets. We do not think that it matters that sometimes decisions of this sort are going to get tricky; it is enough that most of the time they are straightforward – and when they are not, it is not unreasonable that the subjective experience that results is a bit muddled, a bit ambiguous.

Which leads into the more general point that there is a degree of arbitrariness in this dividing up of our world of neurons into nodes and links which will be reflected in the continuous values of statistical indices of node-ness and link-ness. Nevertheless, most of the time we expect to see clear water between nodes and links, and that the summary bottom left of Figure 2 above is a fair one; that we can usefully distinguish between the activation of a node and the activation of the link between two nodes. Similarly, there is a degree of arbitrariness in this dividing up of our nodes into shape nodes and texture nodes, into shape nets and texture nets.

Figure 9

In this example we sketch what might be done with a patch of folded cloth, with fragments of shape net being used to indicate the stronger folds in the cloth, with supplementary topographical information being provided by variations in the texture net – not here shown. We show some of Leonardo da Vinci’s cloth below by way of illustration, similar but not identical to that first shown at reference 10.

Figure 10

Figure 11

Figure 12

While in this penultimate example – Figures 11 and 12 – we illustrate a composite object made up of three layer objects of two parts each, separated by the visually intrusive red elements. The C-links, which are not shown, are however suggested by their green terminals, which may generate the subjective experience of a triangle. See, for example Figure 5a of reference 8.

Figure 13

In Figure 13 we offer a minimalist version, sufficient for present purposes. Time might tell which version suits better.

Figure 14

We associate to scaffolds and scaffold boards, with the scaffold poles being the shape net and the scaffold boards the texture nets.

With the idea being that a bit of shape net only acquires substance from an adjacent texture net, while a bit of texture net only acquires focus and definition from an adjacent bit of shape net. All of which being brought out by the activation processes.

Figure 15

In this last example we revert to a problem which has exercised us before. What best to do with an object which is clearly not planar in a representation which more or less here? We could have used the scaffolding above, but we taken the umbrella as our example.

The first take is that there are four layers, each of which is straightforward enough taken in isolation: the supporting rods; the central pole; the skin of the umbrella and its ribs; and, the shadows of the trees above. With the light behind the umbrella, shadows of the supporting rods are not an issue. A first catch is that the supporting rods are connected to the ribs by the central pole. A minor issue is whether it would be better to have one or two texture nets to the panel, with the point of two being to more clearly delineate the pinked disc strengthening the very centre of the skin, where it joins the central pole.

The second take is that we just make a single layer object of the whole thing, breaking all the different elements out into parts for the subsequent reconstruction of the image in consciousness, without regard to the underlying structure. A first catch with this is that there is some sense of the underlying structure in consciousness. So where is that now to come from?

Huang and Pashler of reference 8 would probably argue that this is all unnecessary because the brain only really worries about a small proportion of the image at a time, portions which are small enough for issues of this sort not to arise – with part of the reason for this being bandwidth, the neural costs of projecting stuff into consciousness. So we might be focussing on just one panel and its two supporting ribs, more or less to the exclusion of the rest of it. We do not agree.

Figure 16

Figure 17

One device which could be used to express the crossings of the ribs and rods, and other crossings involved in the umbrella, is shown in Figure 16 and 17 above. In Figure 16 we have three layer objects. Object A1 has a soft lower boundary, indicating that it is subordinate, that is to say partially occluded by Object B. Object A2 has a soft upper boundary. While in Figure 17, on another layer, we have just one layer object A3 with a column object, marked in red, linking it to object A1 and another linking it to object A2, thus making a composite object which binds the two objects A1 and A2 of the first layer together. Using this device we can have the substance of our picture of an umbrella on one layer, with a number of link objects, tying the various broken elements together, on a second.

A bigger soft box model

Figure 18

The figure above being an elaborated version of Figure 1 at the beginning.

Nodes have position on the cortical sheet, the small, two-dimensional bit of cortical sheet on which LWS-N is expressed. The map node to position is many to one.

We allow a focus of attention, fixed for the duration of a frame of consciousness, where activation will be concentrated, as described above. This focus might be a composite object, a layer object or a part of a layer object. A layer object might be the (entire contents of its) layer. As the focus gets bigger, lower level detail is going to be lost, with the changes to synaptic connections needed to achieve this being part of the compilation process which takes us from one frame to the next. So looking back to the umbrella of Figure 15 above, a switch from the red panel to the assembly holding the supporting rods to the central pole would involve a new frame, not necessarily a total rebuild, but certainly a retuning.

Parts are optional elements of layer objects.

Shape nets are made of shape nodes and shape links, that is to say O-links which connect pairs of shape nodes. Shape nets may or may not define parts. Parts may or may not have texture nets.

A composite object is a maximal set of layer objects connected by C-links. We envisage there being various different types of composite object, with the compositions fulfilling different functions. We might talk of the role of a layer object in a composite object. So one layer object may exist, for example, to provide descriptors for another layer object, existence which expresses the more or less unspoken feeling that I am looking at, for example, a bird.

A layer object is a maximal set of shape nodes and texture nodes connected by O-links. A layer object will always contain at least one shape net and will often contain exactly one. We might exclude very small layer objects and allow them to slip back into the background.

A shape net is a maximal set of shape nodes connected by O-links, that is to say shape links, that is to say O-links which connect pairs of shape nodes.

A texture net is a maximal set of texture nodes connected by O-links, that is to say texture links, that is to say O-links which connect pairs of texture nodes. A texture net is usually connected to a host shape net by one or more O-links.

A part of a layer object can be defined by a minimal loop of shape nodes. Most such loops will contain nothing other than a single texture net, a net which more or less fills the part, more or less densely. There are, however complications, some of which have been exemplified above, with the result that a bit of shape net may be associated with no texture net, one texture net or two texture nets, with the consequences that any one bit of shape net may be associated with no, one or two parts of its host layer object and that it is not possible to analyse a layer object into a set of disjoint and exhaustive parts. But what we can say is that each texture net of a layer object defines a part of that layer object. And that all of the texture nets of a layer object will be separated one from another by bits of shape net and that most of them will have a closed perimeter of shape net. Despite these complications, we believe that the part remains a useful concept, one which is straightforward enough most of the time.

Any one node participates in exactly one net in its layer and the nodes of a layer object are the union of its shape nodes and texture nodes.

It is often not possible, or at least not appropriate, to do everything we want to do within the confines of one layer and C-links are used, as noted above, to link material on one layer with material on another. One reason might be the need (for non-infant humans, if not others) to express something more complicated than a plane image of the visual world. Another might be the need to accommodate more than one modality at a time.

So a layer object on one layer may be linked to a layer object on another by means of a short C-link, a link which we have, in the past, called a column object.

Any one layer object will appear in at most one composite object, but we do allow more than one link between any such pair of layer objects. A composite object will often involve more than the minimum of two layer objects.

After Figure 8 above, we talked a little of arbitrariness. This arbitrariness manifests itself here in that the ideal view of a complex world offered here in the form of rules for a box model is only that, and may sometimes be hard to relate to the facts on the ground, rather in the way that a diagram of a animal cell, to the untutored eye, seems to have very little bearing on that cell as seen through a microscope. The diagram is an idealised version of that cell, reflecting truths which may or may not be well exemplified by the cell in question.

Figure 19

An example of a photograph left and a diagram right, of the same animal, albeit not the same view of same. But which hopefully illustrates the difference between the picture and the diagram – bearing in mind the fact that the photograph is something of a construct too, with all kinds of trickery going into its making.

Other points
At reference 4 we talked of frames, takes and scenes. For present purposes, we suppose the network of nodes and links to be fixed for a frame of consciousness. We also suppose that this fixing does not preclude the predicted movement of objects in the visual scene, movement which we suppose to be expressed in the waves of activation which bring the data to life. Expression which burns up bandwidth (in the jargon of management consultants) and reduces the amount of other information that can be expressed.

We have talked in terms of layer objects being superimposed on a background, without, so far, having attempted to fill in that background. This background is a residual and, for the present anyway, we allow that residual to contain one or more texture nets, possibly some fragments of shape net.

Our model of shape nets and texture nets is essentially two dimensional, but it can be used to describe at least some aspects of three dimensional objects. It could also be extended to describe two dimensional surfaces in three dimensional space.

There is also just one bit of cortical sheet, although many brain structures come in pairs, left and right. And if there were two, maybe the answer is as simple as one being a back up of the other, rather as in a computer system running on mirrored servers. Or then again, maybe not.

Conclusions

We have taken the definition of LWS-N further, in particular its foundation in neurons and the organisation of those neurons into layers and layer objects.

This is cast mainly in terms of a topical, graph theoretic view of the neurons and their synapses occupying our patch of cortical sheet. In consequence, we have only used some of the information which could, at least in theory, be extracted from the firing of neurons. We have not yet used the frequency, and we do not expect to use either the detailed timing or the phasing of that firing. We have not considered other aspects of the behaviour of neurons or indeed that of that part of a bit of cortical sheet which is not neurons.

Our layer objects are presently two dimensional, although we do think about doing rather more, albeit within the confines of a two dimensional substrate.

References

Reference 1: http://psmv3.blogspot.co.uk/2018/01/an-introduction-to-lws-n.html.

Reference 2: http://psmv3.blogspot.co.uk/2017/09/geometry-and-activation-in-world-of.html.

Reference 3: http://psmv3.blogspot.co.uk/2017/07/binding.html.

Reference 4: http://psmv3.blogspot.co.uk/2017/06/on-scenes.html.

Reference 5: http://psmv3.blogspot.co.uk/2017/06/on-elements.html. Of interest here for the way in which it dealt with a layer object partially occluding another. While not dealing with one layer object abutting another.

Reference 6: https://psmv3.blogspot.com/2018/05/a-modest-change-to-layer-objects-of-lws.html. Inter alia, including various examples of layer objects, shape nets and texture nets.

Reference 7: https://psmv3.blogspot.com/2018/05/an-update-on-seeing-red-rectangles.html. A summary of where LWS-N and his friends stood at the end of May 2018.

Reference 8: A Boolean map theory of visual attention – Huang, L., & Pashler, H. – 2007.

Reference 9: Single units and conscious vision - Logothetis, N. K. – 1998.

Reference 10: https://psmv2.blogspot.com/2015/09/abstract-expressionism.html.

Group search key: srd.