Coding for colour

Following the advertisement at reference 2 and a first effort at reference 3, we continue to think about moving the LWS from something like an Excel workbook to something more graph-like, more neuron-like. For the present we denote the old version of LWS by LWS-W, with W for workbook.

And here we fly a kite concerning the way in which we might code visual images for colour in its successor, LWS-N.

Contents

• Some preliminaries
• The ring
• The field
• The preview
• The suspender
• The covering
• Doing the colour
• Conclusions, references etc

Some preliminaries

The examples of graphs which follow are to be understood as the product of the compilation process, not the same thing at all as raw input from the retinas or anywhere else. The graphs provide the substrate for the activation processes which amount to consciousness and have been prepared by a compiler which knows quite a lot about the information, the structures that it is projecting into frames of consciousness.

So the graphs are going to be fairly tidy, although it seems likely that there will be a probabilistic element to compilation, with a certain amount of noise arising therefrom. Not to mention noise arising from activation.

We observe that while we talk loosely about graphs, we are really talking about directed graphs embedded in two or three dimensional Euclidean space, with our patch of cortex being thought of as a patch of two dimensional Euclidean space, albeit partitioned into a small number of cohabiting layers, with these layers defined by the frequency with which the constituent neurons oscillate when activated. In what follows we confine ourselves to a single such layer. And we are as interested in the placement of our vertices and edges in geometrical space as we are in the geometry-free connections between them.

We will take some interest in planar graphs, graphs which can be embedded in a plane without any crossing edges. A concept which is not so interesting in three dimensions as one can always jiggle vertices and edges about to change a crossing into a near miss, a wheeze which does not work in two dimensions.

The ring

Figure 1

Figure 1 shows a directed graph in blue, without arrows, but with a clockwise flow of activity. Every vertex, each blue spot, has at least one inbound edge and at least one outbound edge, usually more in both cases. The graph depicts a circle in two dimensions, a circle with an interior.

The red arrow with vertex, bottom left, stands for the source of the activation, powering up the clockwise rotation. There is no other leakage in and no leakage out, no sink: the rotation is the end in itself and the activation does not go anywhere. It just leaks away into chemical or heat energy in the background.

We might add a requirement that the ring be reasonably tangled up. That it not be planar and it not be possible to more or less partition it into planar sub graphs, perhaps amounting to a bunch of circles rather than a single circle. We might add various other graph flavoured restrictions, or at least suggestions, for example, concerning the number of edges running through a plane section through the ring, which ensure that our ring is robust and reliable.

The field

Figure 2

It might be helpful to define a vector valued function on the plane in which graphs of this sort are embedded.

We define the value of the field at point D in Figure 2 above as a weighted sum of contributions from all the edges, with AB being one such. With, if weights were equal, AB+BA being zero.

The weights are of the form 1/(1+distance*distance), where distance is the distance to the nearest point on the edge. An alternative would have been the distance to the mid point on the edge. Plenty of possibilities here. We don’t think it makes much difference. Maybe some  modelling to tell us how much is needed.

So looking at the edge AB, we have the distance of point C being the length of AC, and that of point F being the length of BF. In the case of D, the distance is the length of the perpendicular to the edge AB, while E is on the boundary between the two cases, as BE is at right angles to AB. In any event, the distance we want is the length of BE.

DD’ is a vector, parallel to AB, of unit length. With the value of the field at D being the weighted sum of the vectors DD’.

In large graphs it may be necessary to put a distance limit on the edges to be included. Something else where some modelling is needed.

In the vicinity of the circle of Figure 1, this field will track the clockwise trajectory when on or near the circle and take small values elsewhere.

Contour maps of such a field over a more complex graph might be revealing and might serve to tell us about the boundaries of objects. Whether such a field could or would be available to the compiler is another matter: would it make use such a field to tune its use of the neurons of LWS? And while such a field might be part of or indicative of the content of consciousness, it would not inform consciousness. By definition LWS is consciousness of itself and so cannot have access to any other machinery.

Such a field would not tell us much about how tangled up our edges were. It tells us whether they are all pointing roughly in the same direction, but not whether they are knotted. A collection of identical rings all occupying much the same space would generate much the same field as one big ring.

The preview

Figure 3

By way of a preview, Figure 3 shows in a diagrammatic way, by extension of the ring of Figure 1, how we might develop objects and their parts, the LWS-N equivalent of the layer objects and their parts of LWS-W, of reference 1. This one being a three part object, with the interiors indicated by the green blobs.

There are lots of neurons to the square millimetre of our patch of cortex and clearly this object and its parts, part of the usually very detailed, subjective visual field, could involve complicated shapes. Maybe it stands for a Bengal tiger, with the break down of this tiger into parts being very much a matter for the UCS and the compiler. Lots of different ways of skinning this particular cat, not to say, in this case, this particular tiger.

The suspender

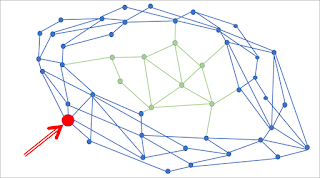Figure 4

With Figure 4 being very much the same as Figure 1, but with the addition of an interior, shown here in green. The green interior being a planar subnet, suspended, as it were, in the interior of the ring.

The catch is that our neurons, these vertices, do not actually do colour. So what do they do instead? The first distinction is that the ring is tightly bound and far from planar, while the subnet is less tightly bound and is planar. The second is that the subnet is only weakly connected to the ring, there is an annulus in which our field takes low values.

The covering

Figure 5

We can cover space in the plane, the interiors of our rings, with three sorts of tilings using regular polygons: the triangle, the square and the hexagon. In the figure above we illustrate the square, distinguished by each interior neuron having four connections, with the connections being more important than the precise placement of the neurons in the plane.

The intensity of the tiling might be measured by the number of neurons. A big intense signal when there are lots of tiles, lot of neurons, a small signal when there are not. This intensity can vary in a continuous way between quite wide limits, it being possible to get lots of neurons in a very small patch of cortex. It can also vary across the interior.

This continuous variation being a necessary condition for doing colour, with humans able to distinguish colours which are very close indeed, provided only that they are next to each other.

Doing the colour

The idea now is that we suspend three planar subnets across the interior of our ring, three subnets which occupy much the same space but which are more or less independent of each other.

Figure 6

One subnet does triangles, one does squares and one does hexagons. Which, given their intensities, gives us something very like the RGB values used in, for example, Microsoft Visual Basic.

But not like RGB values in that we are mapping directly from the firing of the corresponding neurons, the cones, in the retinas, neglecting in this the activity of the far more numerous rods. We are not making use of a coloured dot as an intermediary in this system, the sort of dots you see if you peer at an advertisement hoarding up close and in fact there is no colour of the ordinary sort at all.

Figure 7

Seen from a distance, you get the picture. Click to enlarge and you get the dots.

So we do not suffer from the gamut problem illustrated in the CIE chart which follows, the gamut problem which means that you cannot reach all the visible colours with RGB triples, triples which have to lie on or in the interior of the black triangle.

Figure 8

Some background on all this, rather complicated subject, is to be found at reference 4.

Conclusions

We have exhibited a way in which a sheet of neurons might code for colour. We believe that the necessary information could be held in the way indicated. Whether or not neurons actually do any such thing, or whether their activation would generate the sensation of colour – seeing red as Humphrey would have it at reference 5 – is another matter.

References

Reference 1: http://psmv3.blogspot.co.uk/2017/07/rules-episode-one.html. 

Reference 2: http://psmv3.blogspot.co.uk/2017/08/big-brains.html.

Reference 3: http://psmv3.blogspot.co.uk/2017/09/sensing-spheroids.html.

Reference 4: https://en.wikipedia.org/wiki/SRGB.

Reference 5: Seeing red - a study in consciousness - Humphrey – 2006.

Group search key: srd.